nLab classical double copy
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
Contents
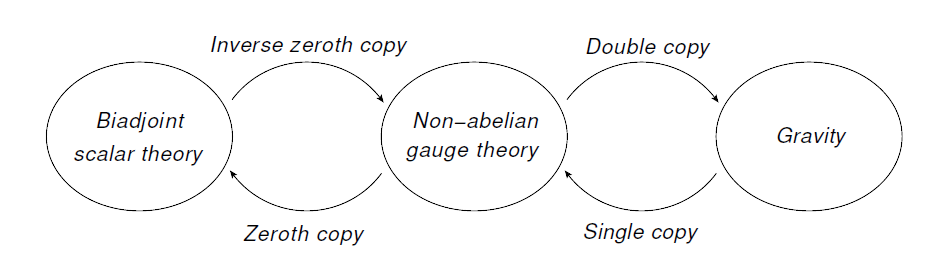
Idea
The classical double copy-method is the counterpart in classical field theory of the double copy-phenomenon for scattering amplitudes in perturbative quantum field theory. It relates classical solutions of the field equations of a Yang-Mills gauge theory with solutions of the Einstein equation in general relativity.
Double copy and classical field theory
Double copy and Kerr-Schild metric
Definitions
-
A Kerr-Schild metric is a perturbation of a flat Minkowski metric of the form
where is a constant with Newton's constant, is a scalar field and is a null covector satisfying the geodesic property, i.e.
-
The single copy gauge field (MOW 15) of this gravitational field is defined for any gauge group by
where is an arbitrary constant color charge, specified by a vector in the basis of the Lie algebra .
-
Conversely, if we start from a gauge field of the form for any constant color charge and null covector satisfying the geodesic property, we can define its double copy gravitational field by the Kerr-Schild metric .
-
Otherwise, if we repeat the procedure of replacing a covector with any fixed color charge we can get a zeroth copy scalar field, defined by
where the new gauge group can be chosen different from the previous .
Field equations
By following (MOW 15) we have a comparison of the field equations. Assume without loss of generality that . We get the following:
-
The vacuum Einstein equations for the metric are (where is the Ricci curvature), which reduce to
-
The Maxwell equations for the gauge field are , which reduce to
-
The Klein-Gordon equation for the scalar field are
Outlook
Summarizing, we have the following table:
| zeroth copy | single copy | double copy |
|---|---|---|
Examples
Examples of classical double copy of gauge fields:
| gauge theory solution | gravity solution | ref. |
|---|---|---|
| electric monopole | Schwarzschild spacetime | (MOW 15) |
| magnetic monopole | massless Taub-NUT spacetime | (LMOW 15, Kim 24b) |
| self-dual dyon | self-dual Taub-NUT space | (Kim 24a) |
| planar wave | pp-wave | (MOW 15) |
| planar shockwave | Aichelburg-Sexl shockwave | (BSW 20) |
Double copy and topology
From (LMOW 15) we know that in terms of charges we have the following correspondence:
| gauge theory solution | gravity solution |
|---|---|
| electric charge | mass |
| magnetic charge | NUT charge |
The topological consequences were explored by (AWW 20):
-
A magnetic monopole is geometrically a principal bundle of the form
which is trivial only on the worldline of the monopole. Therefore, since we have the homotopy , the first Chern class of the bundle will be an element . In other words we have
where is the volume form of and is the quantized magnetic charge.
-
The massless Taub-NUT spacetime with NUT charge is a circle bundle too. In fact it is diffeomorphic to the manifold , where is the -dimensional Lens space with quantized first Chern class . In this case the fiber has the interpretation of time direction, which is periodic and non-trivially fibrated on the sphere of the angular directions.
Therefore the double copy procedure exchange the first Chern class of the magnetic monopole with the one of Taub-NUT spacetime, i.e.
Double copy and Wilson lines
The classical double copy of Wilson lines was introduced by (AWW 20). We can use as gravitational Wilson lines on spacetime the action functional of a test particle. For any loop we can then write
If we assume that the metric is of the form , we can expand at first order in and obtain
where the mass is absorbed into the new parameter . If now we write the holonomy of the single copy gauge field along the same path we get
Thus we immediately see that the double copy rules for a Wilson line are the following:
Notice that they precisely mirror the BCJ prescription of double copy for scattering amplitudes by exchanging color data with kinematic data and gauge coupling constant with its gravitational analogue.
This suggests that this formulation can be a bridge to formally connect classical double copy with double copy for scattering amplitudes.
Double copy and S-duality
In (ABSP 19) it was proved that an electric-magnetic duality (i.e. S-duality) transformation on the single copy gauge fields corresponds to an Ehlers transformation on the double copy gravitational field. In other words the following ideal diagram commutes:
Related concepts
-
string theory results applied elsewhere, open/closed string duality
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
References
Fundamental bibliography:
-
Ricardo Monteiro, Donal O’Connell, Chris D. White, Black holes and the double copy (arXiv:1410.0239)
-
Andrés Luna, Ricardo Monteiro, Donal O’Connell, Chris D. White, The classical double copy for Taub-NUT spacetime (arXiv:1507.01869)
-
Chris D. White, The double copy: gravity from gluons (arXiv:1708.07056)
-
David Berman, Erick Chacón, Andrés Luna, Chris D. White, The self-dual classical double copy, and the Eguchi-Hanson instanton (arXiv:1809.04063)
-
Kwangeon Kim, Kanghoon Lee, Ricardo Monteiro, Isobel Nicholson, David Peinador Veiga, The Classical Double Copy of a Point Charge (arXiv:1912.02177)
-
Nadia Bahjat-Abbas, Ricardo Stark-Muchão, Chris D. White, Monopoles, shockwaves and the classical double copy (arXiv:2001.09918)
-
Joon-Hwi Kim, Single Kerr-Schild Metric for Taub-NUT Instanton (arXiv:2405.09518)
-
Joon-Hwi Kim, Newman-Janis Algorithm from Taub-NUT Instantons (arXiv:2412.19611)
Foundational issues:
- Chris D. White, A Twistorial Foundation for the Classical Double Copy (arXiv:2012.02479)
Some global aspects of the classical double copy were explored in the following paper:
- Luigi Alfonsi, Chris D. White, Sam Wikeley, Topology and Wilson lines: global aspects of the double copy (arXiv:2004.07181)
In the following paper it is shown that a S-duality on a gauge field corresponds to an Ehlers transformation on its double copy:
- Rashid Alawadhi, David Berman, Bill Spence, David Peinador Veiga, S-duality and the Double Copy (arXiv:1911.06797)
The following paper is a proposal of extension of classical double copy to double field theory:
- Kanghoon Lee, Kerr-Schild Double Field Theory and Classical Double Copy (arXiv:1807.08443)
See also:
- Andres Luna, Silvia Nagy, Chris White, The convolutional double copy: a case study with a point (arXiv:2004.11254)
Discussion for D=11 supergravity:
- David Berman, Kwangeon Kim, Kanghoon Lee, The Classical Double Copy for M-theory from a Kerr-Schild Ansatz for Exceptional Field Theory (arXiv:2010.08255)
Description via -algebras:
- Leron Borsten, Branislav Jurčo, Hyungrok Kim, Tommaso Macrelli, Christian Saemann, Martin Wolf, Double copy from homotopy algebras, Fortschritte der Physik, 69 8-9 (2021) 2100075 arXiv:2102.11390, doi:10.1002/prop.202100075
For curved spacetimes:
- Gokhan Alkac, Mehmet Kemal Gumus, Mustafa Tek, The Classical Double Copy in Curved Spacetime (arXiv:2103.06986)
Last revised on March 2, 2025 at 18:24:53. See the history of this page for a list of all contributions to it.